Curious about concavity? The concavity calculator is your go-to tool! Simply input your function, and instantly determine the concavity of the graph. No more guesswork or confusion – get precise results within seconds. Understanding concavity is key in analyzing the shape and behavior of a function. Let the concavity calculator simplify this process for you. Discover the power of this handy tool today!
The Wonder of Concavity Calculators: Exploring Curves and Slopes
Welcome, young mathematicians, to the fascinating world of concavity calculators! Have you ever wondered how we can analyze the shape of curves and slopes in mathematics? Well, that’s where concavity calculators come into play. In this blog post, we will delve into the realm of concavity, explore how concavity calculators work, and discover the magic of understanding curves and slopes. So, grab your thinking caps and let’s embark on this exciting mathematical journey!
Understanding Concavity
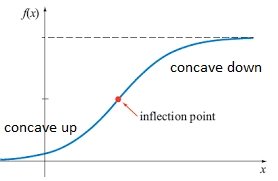
Before we dive into the workings of concavity calculators, let’s first understand what concavity actually means. In mathematics, concavity refers to the shape of a curve or graph. A curve is said to be concave if it curves downward like a frown, while it is convex if it curves upward like a smile. To determine the concavity of a curve, we look at how the curve bends or changes direction.
Now, imagine you have a roller coaster track. As the roller coaster moves along the track, the shape of the track can either be concave, convex, or flat. The track’s concavity affects how the roller coaster speeds up, slows down, or changes direction. Understanding concavity helps us analyze and predict the behavior of curves and slopes in mathematics.
The Role of Concavity Calculators
Concavity calculators are powerful tools that help us analyze the concavity of curves and slopes with precision and accuracy. These calculators use mathematical algorithms to determine whether a curve is concave, convex, or neither. By inputting the necessary data, such as the function or equation of a curve, concavity calculators perform complex calculations in seconds, providing us with valuable insights into the shape of the curve.
Imagine trying to analyze the concavity of a curve manually—it would be a daunting task requiring intricate calculations and a deep understanding of mathematical concepts. However, with the help of concavity calculators, we can simplify this process and focus on interpreting the results to gain a deeper understanding of the curves and slopes we encounter in mathematics.
How Concavity Calculators Work
Now, let’s take a closer look at how concavity calculators actually work. When you enter the equation of a curve into a concavity calculator, it analyzes the curve’s second derivative to determine its concavity. The second derivative of a function provides information about the rate of change of the function’s slope, helping us identify points of inflection where the concavity changes.
Consider a simple curve like a parabola. A concavity calculator will examine the concavity of the parabola by analyzing how the curve bends at different points. If the curve is concave up, the calculator will indicate that the curve is opening upward like a smile. If the curve is concave down, the calculator will show that the curve is opening downward like a frown. Understanding these nuances helps us gain insights into the behavior of curves and slopes.
Practical Applications of Concavity Calculators
Concavity calculators have a wide range of practical applications across various fields, from science and engineering to economics and finance. In physics, concavity calculators are used to analyze the motion of objects, such as projectiles or vehicles, by studying the curvature of their trajectories. In economics, concavity calculators help economists analyze supply and demand curves to make informed decisions about pricing and production.
Furthermore, concavity calculators are invaluable tools in calculus and advanced mathematics, where the analysis of curves and slopes plays a crucial role in solving complex problems. By leveraging the power of concavity calculators, mathematicians and scientists can gain deeper insights into the behavior of mathematical functions and make accurate predictions about real-world phenomena.
Exploring Curves and Slopes with Concavity Calculators
Now that we’ve uncovered the mysteries of concavity calculators, it’s time for you to put your knowledge to the test. Experiment with different functions and equations using online concavity calculators to see how they analyze the concavity of curves in real time. By exploring curves and slopes with concavity calculators, you can develop a better understanding of how mathematical concepts come to life in the world of numbers and shapes.
Remember, mathematics is like a thrilling roller coaster ride—full of twists, turns, and surprises. By mastering the art of concavity and utilizing concavity calculators, you can navigate the twists and turns of mathematical curves with confidence and precision. So, embrace the challenge, embark on new mathematical adventures, and let the magic of concavity calculators guide you through the enchanting world of curves and slopes!
Happy calculating, young mathematicians!
Concavity, Inflection Points, and Second Derivative
Frequently Asked Questions
How does the concavity calculator determine the concavity of a function?
The concavity calculator analyzes the second derivative of a given mathematical function to determine the concavity at specific points. If the second derivative is positive, the function is concave up; if it is negative, the function is concave down.
Can the concavity calculator handle both simple and complex mathematical functions?
Yes, the concavity calculator is designed to handle a wide range of mathematical functions, including both simple linear functions and more complex polynomial functions. It can accurately determine concavity for various types of functions.
How precise are the results provided by the concavity calculator?
The concavity calculator provides precise results based on the mathematical input provided. It calculates the concavity at specific points with a high degree of accuracy, making it a reliable tool for analyzing the concavity of functions.
Is it necessary to have a strong background in calculus to use the concavity calculator?
While a basic understanding of calculus is helpful, you do not need an advanced background in calculus to use the concavity calculator. The tool is user-friendly and provides results in a clear and straightforward manner, making it accessible to users with varying levels of mathematical knowledge.
Final Thoughts
In conclusion, the concavity calculator serves as a valuable tool for analyzing functions’ concavity quickly and accurately. By inputting the function, the calculator effectively determines the concavity intervals, inflection points, and helps visualize the graph. It simplifies the process of identifying concave up, concave down regions, aiding in understanding the function’s behavior. Embrace the convenience of the concavity calculator for efficient curve analysis.